数学《抓核心知识 促认知深化》

抓核心知识 促认知深化

            ——《多边形面积的计算》片段及思考

  南京师范大学附属小学（210018）   张岚

精选课程内容，凸显“核心知识”是当前教育教学改革的发展趋势，“核心知识”的教学就是要让学生在获取知识的同时不断提升自身的素养、发展创新能力和实践能力。数学教学中我们常说的概念、公理、定理、定义、公式、证明……，这些都是数学的组成部分。但是，它们中的任何一个都不是数学的核心所在，数学的核心应该是越过这些表面知识存在的内在技能、思想方法和活动经验。本文就苏教版五年级上册《多边形的面积计算》一课中如何解析核心知识、把握核心思想进行探讨，以期通过对核心知识的理解和学习，帮助学生形成结构性的观点，促进学生从整体上把握知识的学习，初步具备自我生长的能力。

片段一：解析核心、定位目标。

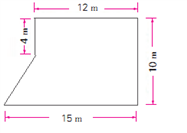
书上的题目是：华丰小学校园里有一块草坪，它的面积是多少平方米？

师：这样的多边形面积你会计算吗？

师：你能转化成我们学过的图形计算出面积吗？

由于学生已经会计算长方形、平行四边形、三角形、梯形面积，所以方法还是比较多样的。

生1：将多边形分为长方形和梯形，分别求出面积再算总和。（图1）

生2：将多边形分成长方形和三角形，分别求出面积再算总和。（图2）

生3：将多边形分成三角形和梯形，分别求出面积再算总和。（图3）

生4：将多边形变成一个完整的长方形，再减去多余的梯形就能求出多边形的面积。（图4）

生5：将多边形变成一个梯形，再减去多余的小三角形就能求出多边形的面积。（图5）

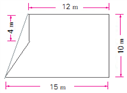
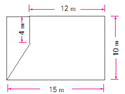
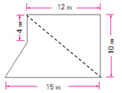
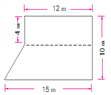
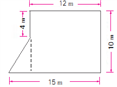
图1           图2             图3           图4             图5

师：这些计算的方法你能分分类吗？

生1：可以分成用加法计算的一类和用减法计算的一类。

生2：可以分成一种在图形内分一分的，一种在图形外加辅助线的。

师小结：同学说的用加法计算的方法就是就是分割的方法，用减法计算的方法就是增补的方法，合起来说就是用到了“割补法”。

在这个教学过程中，教师不能简单地将目标定位在会算面积上，也不能单纯地定位在计算方法的多样化上，如果学生仅仅会利用平行四边形、三角形、梯形面积公式进行组合图形的面积计算与问题解决，那教学就停留在了知识的表层，没有形成真正的数学素养。因此在学生交流各自计算多边形面积的方法后，教师可以提问：“计算的方法你能分分类吗？”有了这样的核心问题，学生就会把将多种方法加以比较，发现这么多种方法无非就是把多边形分成几个学过的图形或者从一个大图形里面减去一个小图形，从而对面积计算的核心知识—— “分割”、“增补”有了充分的感悟与理解。

片段二：把握核心，建构思想。

小学是学生学习数学的启蒙阶段，这一阶段让学生真正理解并掌握一些基本的数学思想显得尤为重要。学生在学习平行四边形、三角形、梯形面积计算时，均是将这些图形转化为学过的图形来计算的。到了组合图形的面积计算更是要加深“转化”的思想方法，把平面图形的知识串成一个整体，形成清晰的知识框架。所以光知道“分割法”还不够，需要进一步分析与理解：

师：这些方法虽然不同那你能看出有什么相同的地方吗？

生1：都用我们学过的图形来解决问题的。

生2：都是把不规则的图形变成规则的图形。

师：这就是“转化”的方法。把不规则的图形转换为规则图形，把未知的知识转化为已知的知识。

师介绍：其实在我们已经学过的知识里很多地方都用到了转化。例如，平行四边形的面积公式是转化为长方形求得的；三角形的面积公式是转化为平行四边形求得的；小数乘法、小数除法转化为整数乘法、整数除法；异分母分数加减法是转化为同分母分数加减法……

课堂教学抓不住数学知识的核心，没有前后一致、贯穿始终的数学思想主线，很容易耗费学生宝贵时间，造成课堂中效益、质量“双低下”。为了让学生在有限的课堂时间里，学到尽可能多的知识，我们要给学生“最有用”的知识，这些知识思维价值大、适用性广、迁移性强。因此在学生总结出计算多边形面积方法的基础上，教师可以生成有价值的问题——“方法虽然不同，但是有什么相同的地方呢？”从而理解“转化”的思想——都是把不规则图形转化成规则图形，把没有学过的知识转化为学过的知识。教师通过挖掘核心知识的本质及其内隐的数学思想，更好地促使教学高效达成目标，而学生的思维也始终在“变”与“不变”；“同”与“不同”的辩证思想中浸润，长期经历这样的磨砺，学生的思考会逐渐走向深入，对其终生学习有着积极的推动作用。

片段三：寻找价值，提升素养。

数学知识和方法的发生、发展通常不会一帆风顺，往往是人们战胜困难和危机的产物。课堂中常常会有似是而非的信息、出人意料的障碍、令人沮丧的困惑。实际上，这些模糊、障碍、困惑也是数学魅力的重要组成部分。一些核心的数学知识和思想也会悄然隐身于上述情境中：它们或能提示突破经验局限或思维障碍的手段，或能暗示改变思维方向的拐点，或能提供逼近问题本质的台阶。

在计算这个图形面积中就有一位学生还介绍了一种方法：从中间找到一个点，将图形分成两个梯形和一个三角形。假设其中一个梯形的上底是4厘米，那三角形的高就是8厘米。如下图：

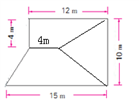
马上就有一个学生说：这样可以分成的话方法就太多了，12除了可以分成4和8外，还可以分成1和11,2和10、3和9……。

还有一个学生说：“这是为了找方法而凑方法。”

这种方法的确有凑方法的嫌疑，如果教师在这里一带而过就浪费了一次很好的教学机会。在这时不妨转变思路来引导学生新的思考：

师：中间的点移动到最右端会变成什么图形？

生：就是将图形分成长方形和梯形。

师：如果移动到最左端呢？

生：就是将图形分成了梯形和三角形，正好是前面同学刚刚介绍的方法。

师：大家看，中间的线我们可以将它不断的移动，当它在中间的时候可以分成三个图形，当线的一端移到最两边的时候就变成了我们前面分成两个图形计算面积的方法了。

在这种看似无用、不合理的方法中教师通过潜移默化的渗透，让学生体验到极限思想的内涵，从而让学生的数学素养得到提升，对数学本质的认识也就更加到位。这样，学生沉淀下来的就不只是数学知识，更主要的是一种数学素养，为他们以后建构新的数学知识体系夯实基础。

“求木之长者,必固其根本;欲流之远者,必浚其泉源。”实践证明，要使学生能长效性发展，获得真正的数学素养与思维能力，就得立足于核心知识的教学。不要十分在意知识的细枝末节，而要厘清知识的内涵和外延，形成和完善的知识结构,体验和领悟理解数学思想方法的本质，让学习的主线更加明晰的展露出来，从而逐步提高独立获取知识和解决问题的能力。

作者：张岚

               单位：南京师范大学附属小学（南京市四牌楼4号）

               邮编：210018

               联系方式：邮箱zhanglan7634@sina.com

手机：13905181156