数学《游戏，让数学变得好玩》

游戏，让数学变得好玩

——简析各版本教材“认识自然数”中的游戏资源

 

2002年，数学大师陈省身先生在为少年儿童的题词中提出“数学好玩”的概念。怎样才能拉近儿童与数学的距离，让数学变得好玩呢？无疑，数学游戏是最重要的载体。

游戏，我们并不陌生，很多一线教师在设计教学时喜欢用小游戏引入教学，也有一些老师在教学中穿插小游戏活跃课堂气氛，还有一些老师尝试用游戏的方式来完成教学。这其中比较经典的有黄爱华老师的《比较数的大小》、华应龙老师的《数字黑洞》、房昔梅老师的《阿拉丁与魔法师》等等。以数学游戏为载体的课堂，让我们看到了孩子的轻松自如，看到了孩子的兴趣盎然，看到了孩子对游戏背后教学内容的体悟。

2011年，《义务教育数学课程标准》修订后，一些教材陆续将数学游戏引入教材，作为教学的组成部分。这是一种变革，更是一种突破。本文以“认识自然数”领域中的数学游戏为例，分析各版本教材中的数学游戏资源。

1.数学游戏——顺应儿童的天性。

玩是儿童的天性。哈佛医学院儿科教授T．贝利·布拉泽顿说：“游戏不只是好玩和刺激而已，它能够激发孩子潜在的创造力和竞争力，是儿童了解世界、了解自己、了解他人与社会最重要的途径。”我们常说，教学中要尊重儿童，用儿童喜欢的方式教儿童学习，教材中加入数学游戏便是对儿童天性的尊重。除了玩，我们认为好奇、好探索、好分享也是儿童的天性。游戏的趣味性，能够引起儿童的好奇心，游戏的对抗性激励着儿童个体的探索，游戏的合作性又催生着儿童的分享。具体来说，儿童对未知世界是好奇的，产生了好奇心，总希望自己一探究竟。探究到什么时候为止呢？自己心里得到澄明和慰藉才肯罢休。我们都有过游戏的经验，在游戏中，儿童总是会缠着小伙伴或成人不断的进行或重复着游戏，直到心理得到满足为止，儿童心理满足的过程，也是认知不断发展的过程。心理获得满足的小伙伴，会把成功的经验迫不及待的和其他人分享，以取得同伴的认可，品尝成功的喜悦，或者在同伴间的分享中将自己的思考发展和提升。

2.数学游戏——引领儿童的认知。

皮亚杰认知发展阶段理论认为，7-11岁的儿童处于具体运算阶段，儿童只能利用具体的事物、物体或过程来进行思维和运算。因此低年级的数学教学，不可能靠教师一味的讲解、引导，更不可能通过大量的题海练习来实现。游戏活动是低年级孩子学习数学、探究数学世界的最重要的方式之一。仔细翻阅教材，发现教材中出现了以下几类游戏：

（1）课前的感受类游戏。

数数是认数的基础。数学家华罗庚曾经说过：“数来源于数（shǔ  ）。”在认识100以内的数之前，北师大版教材安排了《数花生》的游戏活动，让学生经历数数的过程，初步感知一百有多少。游戏分为三个层次：1.放手让学生独立数数。数一数花生有多少个，让学生在数的过程中了解一百以内数的顺序。2.数的对吗？安排再数一次的活动，一方面帮助学生养成检查的习惯，另一方面启发学生可以两个两个的数，结果也是一样的。3.换一种方法，再数一数。在独立数数的基础上，启发学生用多种方法数数：五个五个或十个十个地数。三个层次的游戏活动不断引导学生经历数的过程，层层递进，步步提高。这是基于儿童已有经验，着眼于发展儿童能力的教学。儿童在自主的游戏活动中，习得了知识，积累了数数的经验。

（2）课中的巩固类游戏。

皮亚杰认为，游戏作为一种不平衡状态，它的同化作用大于顺应作用，所以可以通过游戏来练习和巩固刚刚习得的知识。在《认识万以内的数》时，北师大版教材和人教版教材分别设计下列游戏：

 

 

 

 

 

 

 

 

 

 

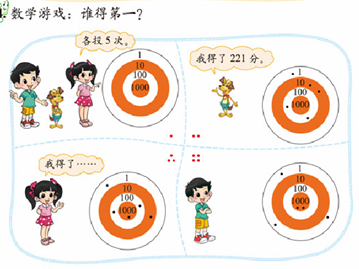
（北师大版教材二年级下册第26页）

 

 

 

 

 

 

 

 

 

 

 

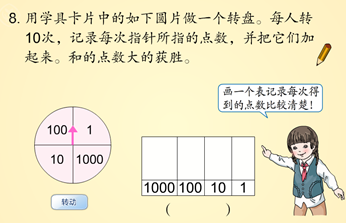
（人教版教材二年级下册第93页）

 

 

这两个游戏的设计有异曲同工之妙，利用游戏巩固了数的组成和数的大小比较。同时，也为后面学习整百、整千数的加法进行铺垫，初步渗透“只有相同单位才能直接相加”的道理。

（3）探究类游戏。

教学不是简单的师传生授，很多知识和经验的获得（尤其是对策略和规律的把握），需要学生在多样化的操作活动中去感受和领悟，进而达到运用的高度。数学游戏除了能帮助学生感受知识、巩固认知以外，还在学生综合能力的发展上起着非常重要的作用。探究类游戏正是学生综合能力发展的载体。

    北师大版教材在《认识万以内的数》时，安排了如下的游戏：

 

 

 

 

 

 

 

 

 

 

 

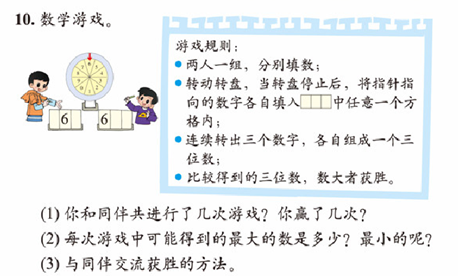
（北师大版教材二年级下册第33页）

 

 

 

这个游戏分三个层次。第一层次，让学生转动转盘，填出三位数，然后比较数的大小。第二层次，统计游戏中获胜的次数。第三层次，思考并与同伴交流获胜的方法。游戏的目的不仅仅是巩固对数的大小的认识和比较方法，而是通过统计的过程引导学生反思：怎样才能获得游戏的胜利？学生在偶然性获胜与必然性获胜的多次游戏尝试中，发现：要想赢得游戏，一定要把最大的数字放在最高位上，可由于转转盘的随机性，学生无法预测下一次会转到什么数字，因此还要考虑如何安排获胜的可能性更大些。多次的游戏使得学生逐步探究出获胜的策略，也可以感悟偶然事件有时会影响最终的游戏结果。学生反思与分享的过程就是学生不断积淀数学活动经验的过程。看似简单的游戏背后，蕴含着丰富的策略，这需要学生在游戏中去探究、体悟。

当然，这里的探究，除了探究某一结论、体悟策略之外，还有对规律的发现，验证和应用。

人教版教材在一年级上册《认识100以内的数》以后，安排了下面的游戏活动。

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

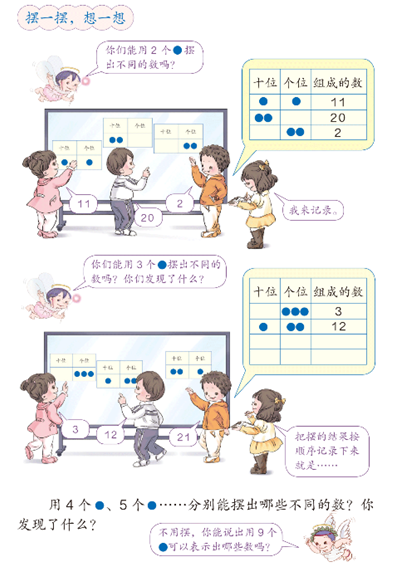
（人教版教材一年级下册第51页）

 

 

 

    游戏通过“用圆片在数位表上摆出不同的数”的活动，巩固学生对100以内数的认识，体验位值制思想，更重要的是让学生在游戏中根据圆片个数与所摆出的数的个数之间的关系，发现规律、运用规律。在游戏中，体会有序思考的价值，感受到数学的“好玩”。游戏分为4个层次。第一层次是用2个圆片摆出不同的数，并记录。通过这个层次的探索，让学生知道每个圆片摆在不同的位置就表示不同的数，初步感受“位值”。第二层次，用3个圆片摆出不同的数，通过这个层次的探索操作，进一步感受“位值”，优化方法，体悟有序思考的好处。第三层次，用4个、5个乃至更多的圆片摆数，在操作中发现、总结其中蕴含的规律。第四层次，综合运用所发现的规律解决“用9个圆片可以表示出哪些数？”的问题，体现了由直观到抽象的层次，体会规律的重要性。

    本节课蕴含的规律不是教师告知的，也不是少数几个优秀学生的展示，而是在层层递进的游戏设计中，学生个体或小组自主的探索和发现，通过与其他小组的交流，或是验证规律或是完善规律。游戏发展了学生有序思考意识，培养了学生探索、归纳并应用规律的能力。

（4）阶段综合类游戏。

除了课前进行的感受类游戏外，课中的巩固类游戏，还有学完一个版块后的综合性游戏。人教版教材在《认识11-20》后安排了《数学乐园》活动。活动以“下棋”游戏的方式，两人对弈，巩固所学知识，体会知识间的联系。

 

 

 

 

 

 

 

 

 

 

 

 

 

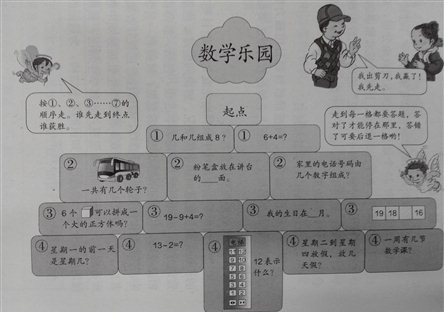
（人教版教材一年级上册第82页）

开展游戏时，准备好磁力贴，一面写题目，另一面写题号，按照题号的顺序先翻题再进行答题，解答后游戏双方互相评判一下解答的是否正确。

这个游戏有着明确的游戏规则：①两人一组，猜拳决定谁先走。②按①、②、③……的顺序走，谁先走到终点谁获胜。③走到每一格都要答题，答对了停在那一格，答错了后退一格。

明确的游戏规则，丰富的游戏体验，以及游戏的对抗性使得学生更加积极主动的投入学习，轻松掌握所学的知识。

仔细研究上面几个游戏，每个游戏都有着明确的教学目标，但是游戏的着眼点却不仅限于一节课的学习，都自觉不自觉的为后续学习孕伏。

这些数学游戏对于低年级学生来说是学生发现数学乐趣的窗口，是带领孩子走向数学教学殿堂的途径之一。它对于培养学生的学习兴趣、调动学生的学习积极性有着积极的影响。学生在游戏中不断丰富着对数的认知。

3.数学游戏——体悟思想方法。

《义务教育数学课程标准（2011版）》明确的将“基本思想”作为“四基”之一。和“基础知识”不同，“基本思想”不能通过教师的讲授获得，只能以数学游戏和数学活动为载体，通过学生的动手操作、探究活动来来渗透。学生在多样化的游戏活动中，慢慢的体悟。

在《认识万以内的数》时，北师大版教材安排了下列数学游戏：

 

 

 

 

 

 

 

 

 

 

 

 

 

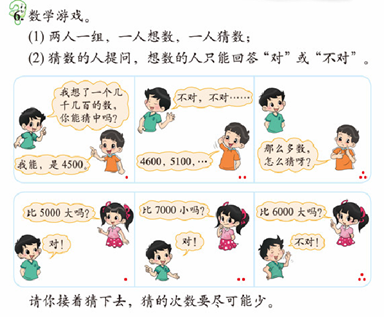
（北师大版教材二年级下册第29页）

 

 

 

这个游戏通过大数的比较发展学生的估计意识和估计策略，游戏运用了逐步逼近的思想。通过这样的游戏，加深学生对数的大小的体会，在猜的过程中，一开始学生的猜是漫无目的的，然后在猜的过程中不断的积累猜的经验，根据对方的应答不断的调整猜数的方向，修正原有的认识，并在活动中逐步认识“区间套”的方法，逐步逼近正确的答案。猜数游戏可以多次进行，重复的猜数游戏，使得学生不断的思考、调整猜数的策略。在小组游戏的基础上，教师可以组织全班同学交流他们猜数的成功经验，在交流和分享中，学生的猜数经验得以丰富和深化，也体悟了逐步逼近的思想。

 

数学游戏走进教材，让数学变得生动和有趣，为数学教学注入一股新鲜活力，也为我们实施数学游戏和深入研究打开了一扇窗。教材中的数学游戏作为一种新生事物，必然存在着一些不足。反思教材中的数学游戏，主要存在以下不足：1.散点式分布，根据教学内容随意设计，更多的是作为具体教学内容的附属品，没有形成体系。如此的游戏设计，容易被一线教师忽略，仅把它当做饭后的甜点，发挥不了应有的作用。2游戏与活动的界限模糊。3.游戏内容的思维含量、挑战性有待加强。

如何让数学游戏更好的为学生的发展服务，体现它应有的价值呢？唯一路径是：让游戏更像游戏。结合前人的研究和小学生的年龄特征，我们认为，数学游戏应该包含四个方面的要素：明确的游戏规则、适当的游戏障碍、真切的游戏体验、激烈的游戏竞争。如果教材中的游戏设计朝着这个方向努力，相信它一定会大放异彩！